
The problem of the sofa, which has haunted mathematicians and the characters of the TV series “Friends” for decades, has finally been solved
The mathematical problem, which is a two-dimensional modeling of a real-life problem of moving a sofa in an apartment or house, has finally been solved. It first appeared in 1966 and has been a source of puzzlement for mathematicians and the characters of the Friends TV series.
This problem defines the largest sofa that can fit around a corner of a given width, a problem that the characters of the show faced in an episode that aired in 1999. A mathematician from South Korea has found a solution to this problem and published his results on the ArXiv preprint server, Live Science reports.
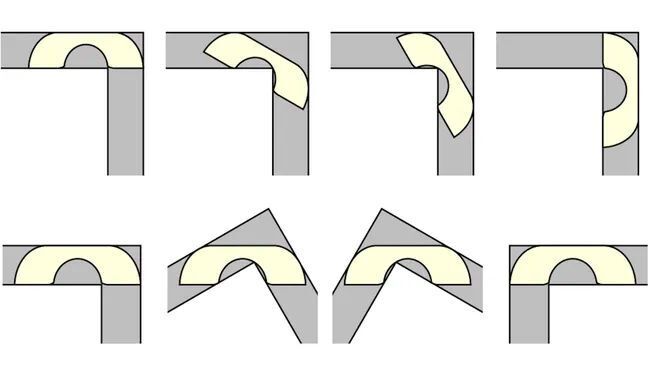
The problem was formulated by the Austrian-Canadian mathematician Leo Moser. He asked about the largest possible area of a single shape in one plane that could move around a right-angled corner of a corridor with a unit width. At first glance, it may seem easy, but in fact, it is not, because the task involves both calculating the maximum area and moving the shape.
And now, on December 2, Jineon Baek, a doctoral student in mathematics at Yonsei University in South Korea, has found a solution, which he published in a little over 100 pages of mathematical proofs. Baek found that for a hallway 1 unit wide, the maximum area of an imaginary sofa could be 2.2195 units – narrowing the answer to within the previously known range of 2.2195 to 2.37 units. The proof has not yet been published in a peer-reviewed journal and will need to be worked out by other mathematicians to determine that it is indeed optimal.
In 1992, mathematician Joseph Gerwer of Rutgers University set the lower bound for a sofa at 2.2195 units. But years of debate over whether a sofa could have a larger area led an international group of mathematicians in 2018 to suggest that the upper limit for the maximum area of a sofa is 2.37 units.
That is, Ross could have avoided the problem if he had only considered the Gerver sofa with 18 curved sections and a maximum area of 2.2195 units.
The Gerver sofa is a wide U-shaped sofa with a curved “seat” that can squeeze around a corner without hanging up. The question was whether this carefully designed sofa, made of 18 individual curves, was really the largest and most optimal shape that could change. Beck worked out the geometry of the shape and its movement and found that Gerwer’s solution was in fact correct.


Comments (0)